Dans cet article nous allons découvrir les limites des méthodes de calcul du poids idéal quand on est grand. Nous comprendront ensuite pourquoi ces formules et calculs ne fonctionnent pas. Enfin, nous verrons des mises en application imagées de ces mêmes logiques dans le règne animal. Bonne lecture !

1. Préambule
Il existe de nombreuses manière de calculer son poids idéal. Nous allons dans cet article voir quelles sont les méthodes classique et pourquoi elles sont limités quand on est grands. Ensuite nous découvrirons d’autres manières de mieux comprendre son poids quand on est une personne de grande taille.
A. Via les formules
Ces notions de calculs de poids idéal rencontrent de nombreux biais. Par exemple une personne très musclée passera pour obèse d’après les formules suivantes ou d’après les formules d’Indice de Masse Corporelle (IMC) ou d’Indice de Masse Graisseuse (IMG).
Idem pour les personnes de petite taille, plus on s’éloigne des standards de taille moins ces formules sont pertinentes, on découvrira pourquoi plus loin dans l’article.
Il est à noter également que le bien être physique d’une personne ne devrait pas se réduire à une formule mais à un ressenti dans la vie de tous les jours.
B. Via les outils
Pour ceux qui souhaitent analyser ou connaître leur poids le plus adapté de manière sérieuse, le mieux est de regarder le taux de graisse. Car c’est le seul indicateur concret permettant de valider une perte de poids saine. Pour cela rien ne vaut un rendez-vous avec un médecin spécialisé ! Celui ci utilisera des outils professionnels adaptés pour calculer le taux de graisse.
Pour ceux qui veulent avoir des informations approximatives sur son poids la solution de la balance impédancemètre peut être adaptée. Elle vous donnera toutes sortes de statistiques sur votre % de graisse, de muscle, d’eau, etc. Cependant elles ne seraient pas très fiables et sont peu adaptées aux personnes très musclées.
Enfin, le meilleur outil est la pince à pli cutanée. C’est celle qui est utilisée par le médecin qui vient pincer à divers endroits notre graisse afin d’en mesurer son épaisseur. Ensuite un total est fait, et en fonction de votre âge et de votre sexe vous avez votre taux de graisse. C’est la méthode abordable la plus efficace.
Découvrons à présent les méthodes de calculs rapides et classiques avant d’aller plus loin sur les limites de ces formules pour les grands.
2. Les méthodes classiques
Ces méthodes ont pour objectif de calculer un poids idéal par rapport à sa taille. Il existe 3 méthodes de calcul classique:
A. Formule de Broca
La plus simple est la formule de Broca. Elle consiste à enlever 100 à sa taille en centimètre:
Taille (en centimètres) – 100 = poids idéal en kilos
Par exemple, une personne mesurant 1m80 (180cm) aura pour poids idéal: 180-100=80kg.
Il existe une marge d’erreur de 15% pour les hommes et de 10% pour les femmes.
Une personne de 2m10 devrait ainsi idéalement peser 100kg. Ce qui n’est pas trop trop surprenant encore.
B. Formule de Lorentz
Deuxième formule assez simple: la formule de Lorentz, elle est plus avancée que la précédente et se présente comme suit:
Homme: Taille en centimètre – 100 – ((taille en cm−150)/4)
Cela donne pour un homme de 1m90:
190 – 100 – (( 190 – 150)/4) = 80kg
Pour une personne de 2m10 ça donnerait ceci:
210 – 100 – (( 210 – 150)/4) = 90 kg
On commence à voir les limites de cette formule pour les plus grands.
Pour les femmes la formule est la suivante:
Femmes: Taille en cm − 100 − ((taille en cm−150)/2,5)
Cela donne pour une femme de 1m80:
180 – 100 – (180-150)/2,5 = 68kg
C. Formule de Creff
Enfin, troisième formule, un peu plus sophistiquée, la formule de Creff. Sa particularité est de prendre en compte la morphologie de la personne:
Taille en centimètre – 100 + K x (9/100) x âge
K correspond à la morphologie:
- 0,9 pour les minces
- 1 pour les moyenne
- 1,1 pour les larges
Cela donne pour une personne de 1m90, de 30 ans à morphologie normale:
190 – 100 + 1 x (9/100) x 30 = 92,7kg. Le résultat dénote assez des autres avec une tendance à la hausse.
Et pour une personne de 2m10 du même âge, même morphologie:
210 – 100 + 1 x (9/100) x 30 = 112,7kg
Elle semble plus adaptée que les précédentes pour les plus grands. Découvrons maintenant pourquoi.
D. Les graphiques d’indice de masse corporel
Pour conclure cet partie, découvrons différents graphiques de l’indice de masse corporelle généralement utilisés par les professionnels:
Graphique d’IMC classique

Ce graphique est assez représentatif des formules susnommées si l’on a un gabarit normal. En revanche, dès lors qu’on est un peu costaud (carré ou musclé) on s’aperçoit que dans les grandes tailles ça devient inadapté.
En voici un autre lié à l’indice de masse corporelle plus complet (en anglais):
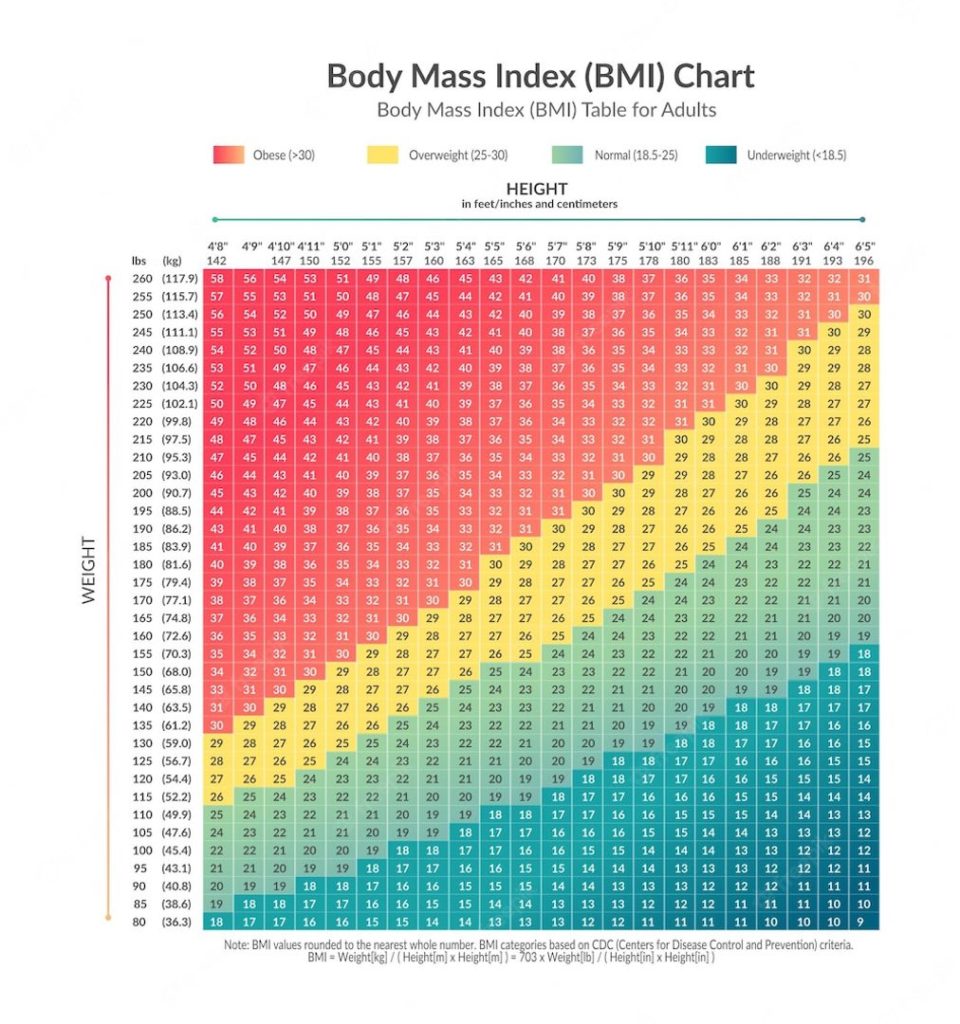
Enfin, voici une version française personnalisée pour les personnes de grande taille (cliquez sur l’image pour mieux voir):
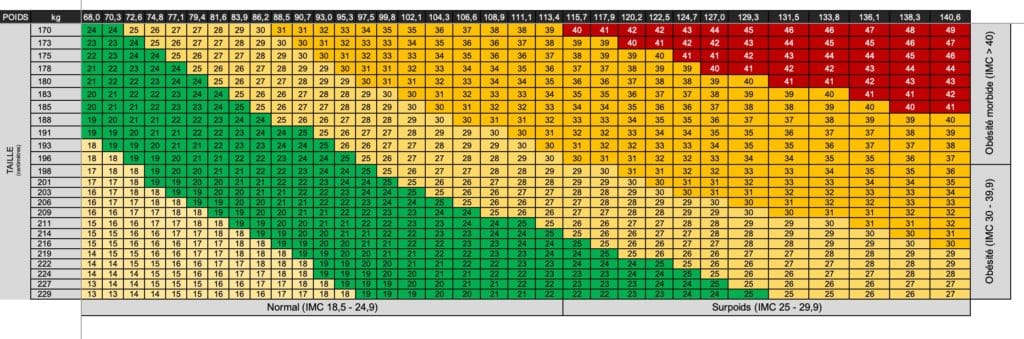
On s’aperçoit dans ce graphique que plus on est grand moins la logique s’applique et plus il semble compliqué d’appliquer la formule de calcul de l’Indice de Masse Corporelle qui est:
IMC = poids (kg) / (taille (cm) x taille (cm))
3. Pourquoi les grands peuvent être proportionnellement plus lourds ?
La raison pour laquelle les grands sont proportionnellement plus lourds que les personnes de taille normale tient en une raison : La règle carré-cube
A. Qu’est ce que la règle carré cube ?
Cette règle, également appelée effet d’échelle, s’applique au monde du vivant, ainsi qu’à toutes les constructions existantes.
Elle consiste à dire que le volume d’un objet augmente proportionnellement plus vite que sa taille. Pour un cube, si la face multiplie sa taille par deux, son poids sera lui multiplié par huit (cf visuel ci dessous)
En clair, cela s’explique par le fait que le volume en 3 dimensions est proportionnel au cube de la hauteur, tandis que la surface en 2 dimensions est simplement proportionnelle au carré de la hauteur.
Et cela à un impact direct sur le poids
Explication en image :
Si cela n’est toujours pas clair je vous invite à visionner cette vidéo explicite (en anglais):
B. Comment la loi carré cube s’applique à l’homme ?
Cette logique s’applique à une forme cubique. Nous, les humains, ne sommes pas des cubes, nous sommes plus proches du parallélépipède ou du cylindre.

Et, si l’on réalise les calculs pour une faible prise de tour de poitrine (pour les hommes par exemple) à mesure que la taille augmente, on s’aperçoit que le gain de masse reste linéaire et que la loi carré-cube ne s’applique que très peu.
Démonstration:
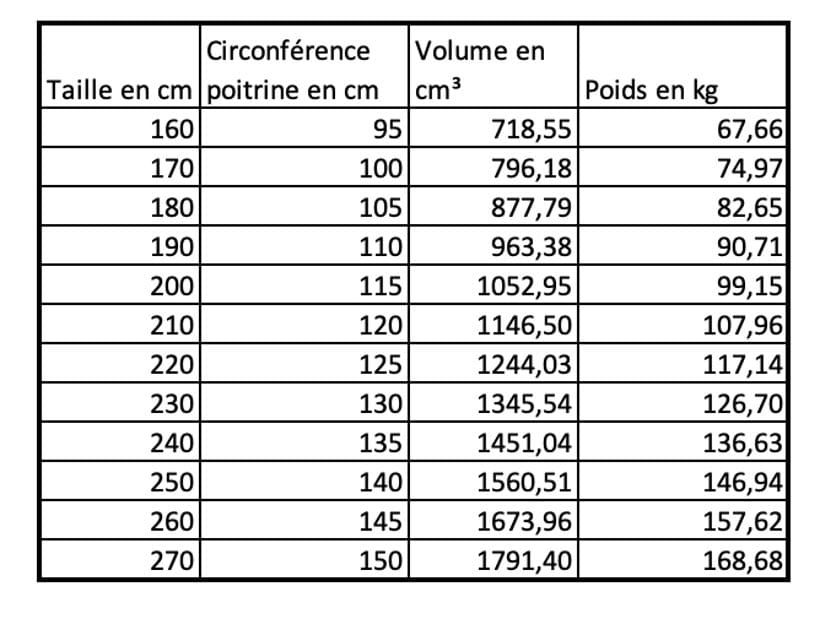
Le tableau suivant se base sur des tours de poitrine classiques pour un gabarit normal. En l’occurrence du XXL a été attribué pour 2m10 soit 120cm de tour de poitrine à morphologie banale. Ensuite on a extrapolé en suivant la logique des tailles inférieures.
Pour le calcul du volume en cm³ nous avons appliqué des logiques de calcul de volume cylindrique (avec les biais que cela comporte). A savoir le calcul de l’aire en se basant sur la circonférence puis en multipliant par la hauteur: 𝜋 x (circonférence/2𝜋)²
Et enfin, pour transformer le volume en cm³ en poids en kilos, nous avons multiplié par la densité du corps humain qui est de 1062 kg/m³ et avons divisé par 100 car nous partions de centimètres et non de mètres.
Le résultat donne ceci:
Les résultats démontrent que plus on grandit plus l’écart se réduit entre taille et poids (« idéal »).
C. Comment la loi s’applique à quelqu’un de très grand ?
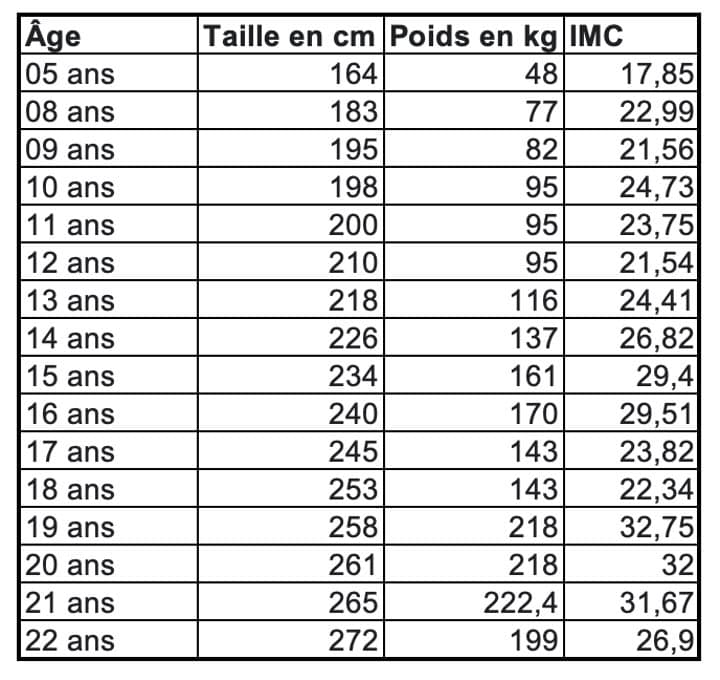
En revanche, celle-ci s’applique de plus en plus si la personne prend de la taille. On peut le voir de manière simple avec Robert Wadlow, l’homme le plus grand de tous les temps qui n’a jamais été spécialement “fort”.
On peut voir que la logique du carré cube s’applique pleinement:
Ici en superposant l’échelle linéaire précédente et celle de Robert Wadlow:

Robert Wadlow pesait ainsi 200 kg pour 2m72. Alors que la logique aurait voulu qu’il pèse 172 kg environ (272-100), pourtant, comme en atteste ces images il était (très) filiforme:

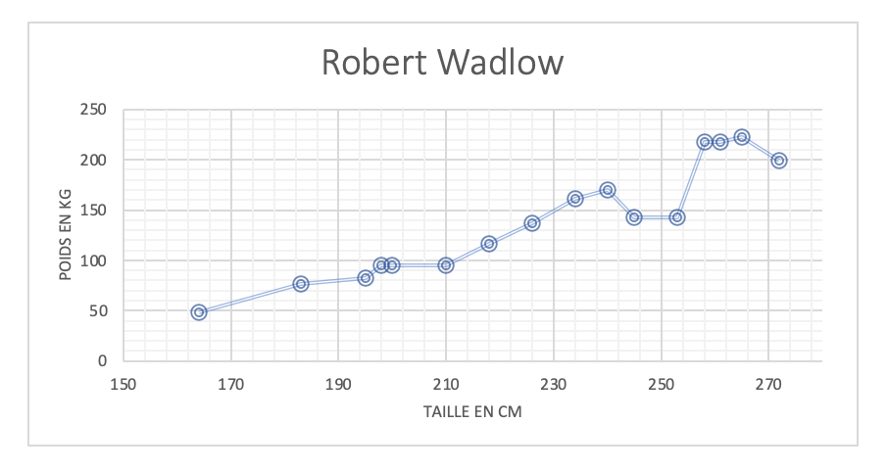
On le voit d’autant mieux sur ce graphique:
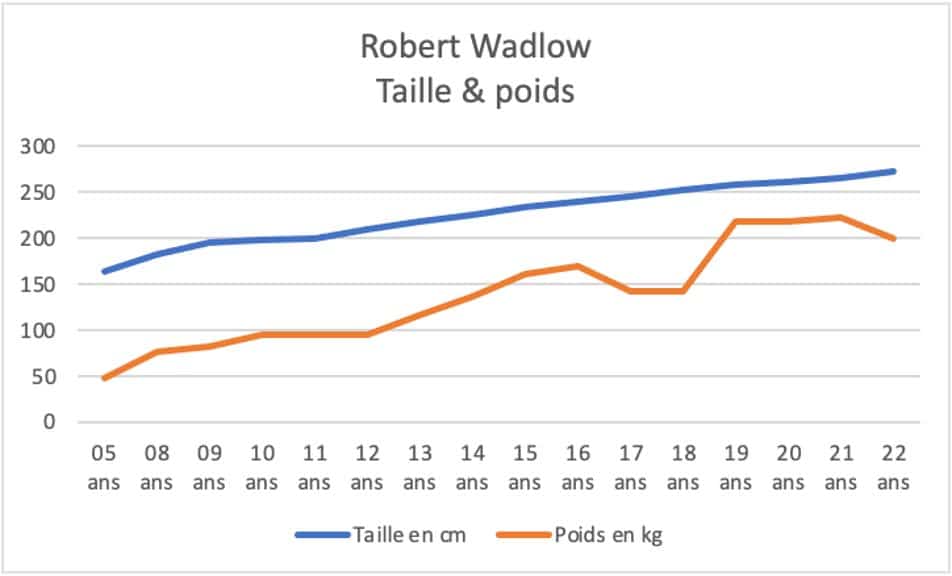
Au fil de sa croissance l’écart se réduit entre taille et poids.
Autre exemple explicite, celui de l’ex-basketteur chinois Yao Ming. Il mesurait 2m29 et n’a jamais été en surpoids. Pourtant il pesait 141 kg (contre 119kg d’après certaines formules de calcul de poids idéal). Voici un cliché du joueur:

Nous poursuivrons dans la partie suivante avec d’autres exemples imagés afin de comprendre l’implication de la loi carré cube.
4. Les preuves en images
Voyons à présent quelques mises en application chez les humains costauds et animaux pour mettre en exergue la logique de la loi carré cube.
A. Strongman géant vs champion de Crossfit
Tout d’abord commençons par un comparatif intéressant. Dans l’image qui suit vous verrez que Thor Bjornsson (ex-Strongman et acteur dans Game of Thrones) et Matt Fraser ( multiple vainqueur des Crossfit games) ont la même silhouette (à peu de choses près):

Les proportions musculaires et physiques des deux athlètes semblent (plus ou moins) identiques. On pourrait donc penser qu’il ont le même ratio taille poids. Or il n’en est rien.
Voici leurs mensurations respectives:
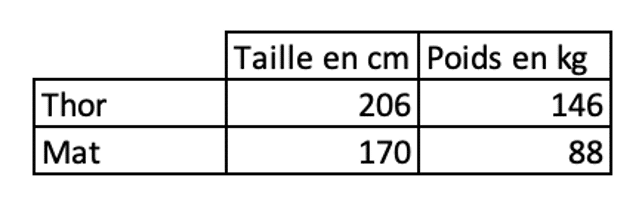
La différence est conséquente. Mat est à +18 par rapport à sa taille alors que Thor est à +40.
De plus, Thor fait 36 cm de plus que Mat, alors qu’il pèse 58kg de plus !
On retrouve ici pleinement la logique de la loi carré cube. Un grand qui grossit de manière visuellement croissante par rapport à quelqu’un de taille normale, prendra du poids de manière non pas croissance mais exponentielle, la faute à la logique du calcul au cube et non au carré.
Les images sans le montage:

Voyons à présent si cette logique s’applique chez les animaux, qui sont des êtres vivants également et ont la particularité d’être beaucoup plus grand que les humains et parfois beaucoup plus lourds.
B. La loi carré cube chez les ours
Nous allons découvrir que la loi carré-cube s’applique également au règne animal. Découvrons ici des comparaisons entre différentes familles d’ours. En partant du principe qu’il ont la même densité et la même physionomie entre eux, nous allons vérifier si la règle carré-cube s’applique ou non:

On voit qu’elle s’applique pleinement. Plus l’objet (ou humain ou animal) est grand, plus la loi a de l’impact. Dans l’exemple présent on voit nettement que l’évolution de la taille entre les espèces est linéaire alors que le poids est davantage exponentiel, comme le montre ce graphique:

C. La loi carré cube chez les requins
Faisons de même chez les requins de même physiologie pour voir si la règle s’applique également:


Bien que les exemples manquent on s’aperçoit tout de même que la règle est respectée. Il y aurait sans doute des éléments à approfondir par rapport aux particularités de l’eau qui facilite le mouvement chez les poids très lourds (et qui explique le poids de certains requins).
D. La loi carré cube chez les félins
Voyons pour conclure la partie animalière, un dernier exemple avec des félins, toujours à physiologie similaire:


On s’aperçoit ici que tant que le gabarit est “petit”, à savoir moins de 1m80, la loi carré cube ne s’applique pas. En revanche, dès qu’on augmente la taille du félin, son poids explose.
Ceci vient encore une fois renforcer la logique de prise de poids non proportionnelle à physiologie égale.
Montage entre un tigre de sibérie et un chat (deux extrêmes du tableau précédent)


5. Pour conclure
Vous avez pu constater que le calcul du poids idéal n’est pas toujours simple quand on est grand. Si les formules classiques peuvent suffire en cas de morphologie banale, on s’aperçoit qu’elles s’éloignent très vite de la réalité dès lors qu’on prend du poids (graisse ou muscle).
Nous avons ensuite compris pourquoi les formules déraillaient autant. La faute en incombe à la fameuse loi carré-cube, qui fait augmenter l’aire d’une surface au carré alors que son volume (et donc poids) progresse au cube.
Enfin nous avons pu observer en image que cette loi s’appliquait aussi au monde animal, à travers l’analyse d’ours, requins et félins.
Nous aurions pu pousser davantage la recherche de calcul idéal pour les grands en essayant de trouver une formule précise pour calculer le poids mais ce n’est pas l’objet de l’article et la formule aurait dû être trop sophistiquée pour être pertinente et applicable. Le but de l’article est d’avant tout faire comprendre la logique globale de la loi carré cube appliqué aux êtres vivants. Un futur article, plus orienté formule idéale sera peut-être publié.
On espère que cet article vous a plu, n’oubliez pas que quelque soit votre poids l’important est d’être bien dans sa peau et que les méthodes de calculs du poids idéal ne remplaceront jamais un bon RDV chez le médecin !
Merci également à Mickaël pour le coup d’œil scientifique !
Articles de la même catégorie:
- Quel pays à la plus grande….taille moyenne
- Quels facteurs déterminent notre taille ?
- L’évolution de la taille moyenne des adolescents depuis 30 ans
- Pourquoi la taille moyenne du pays le plus grand du monde diminue ?
Et pensez à nous suivre sur facebook pour ne rater aucune actu ou bon plan !